t is sometimes confusing to compare investments because different markets have different conventions for quoting interest rates. One way to cut through the confusion is to translate the problem into some implied sequence of cash flows over time. Therefore, when you compare securities in markets that use different conventions, it is important that you first translate the convention into the implied amounts and the timing of the contracted cash flows so you may draw a meaningful conclusion.

There are two main conventions for interest computations:

1. Compound interest

2. Simple fractional interest

Generally, interest is quoted in an annualized form. The period to which it is applied can be any period, such as daily, weekly, monthly, or semiannually. Accepted practice for what constitutes a year or a month also varies so that a year can be 365 days, 364 days, or 360 days, and a month is sometimes standardized to 30 days.

Suppose interest is quoted as r% per annum, compounded monthly, and Method 1 (compound interest) is used. The interest revenue from an investment of $95 for one month is:

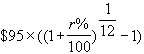
If r% = 12, the interest revenue, to the nearest cent, equals $0.90.

Using Method 2, simple fractional interest, interest is computed as:

If r% = 12, the interest revenue equals $0.95.

These two forms of interest are computed on an "add-on" basis. That is, the yield is stated as a percentage of some deposited amount. For example, Eurodollareur_irf deposits are quoted in terms of simple fractional add-on interest relative to the amount invested.

Other rates are quoted by applying either compound or simple interest to a price paid relative to defined future amounts. That is, the future value is well defined, and the yield is quoted as a discount from this face value in either compound or simple interest form. This is sometimes referred to as a "discount yield."

If interest is quoted as a percentage per year r%, as it often is, the relationship between price and a (simple) discount yield is:

where P is price, F is the face amount, r% is the discount yield, t is the number of days to maturity, and DY is the relevant convention for the number of days in the year.

If r% = 12, F = $100, t = 180, and DY = 360, the price P = $94

Another interest term is the bond equivalent yield. This is an add-on variation of the discount yield. It is expressed relative to the price, not the face value, and it can use a different convention for the number of days.

The bond equivalent yield, r%, is defined as:

In the above example, the bond equivalent yield is (6/94)*200 = 12.76596

Some of these terms can be confusing. When we describe particular securities (such as Treasury bills) and the specific convention used to quote interest rates for them (such as discount yield), the concepts should become clearer.

No matter what the convention, the basic principles discussed in Topic 1.4, The Calculation of Interestcoi_tvm, always apply. For contrasting different opportunities, you can always reconstruct the timeline for cash flows implied by a particular convention for a particular opportunity. Different opportunities and their different conventions, when reduced to each timeline, can then be compared using the same interest rate convention.

The Treasury Calculator included as software in Bond Tutor can translate most of these conventions into simpler terms, such as yields or dollar prices. Online, you can access the Treasury Calculator below. This appears as follows:

You can select the Treasury Instrument from the tabs. Once this information is specified, the bond equivalent yield (BEY) and/or yield to maturity are computed.

Daycounts and date calculations are most important when working with Treasury securities.  As a result, at the bottom of the calculator above allows you to compute day counts for any pair of dates. Once you click Calculator, the number of days is computed. You can automatically transfer this number to the fields for the Calculator you have open above by clicking on the Transfer button. 

Example:  In the example below, a current Treasury Bill has a maturity date equal to 6/9/2011.  This date is entered as below:

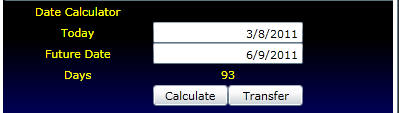
By clicking on Transfer the day count is automatically transferred to the Treasury Bill calculator:

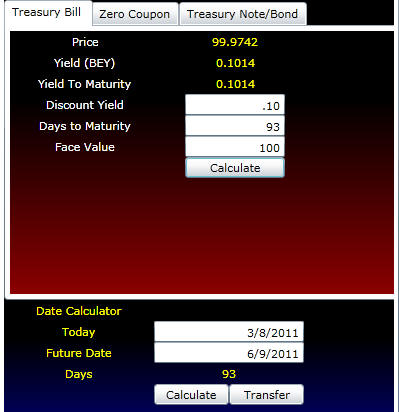
Online you can try it out for different types of instruments, including the current 3 month Treasury bill and the 10 Year Treasury constant maturity bond.

To learn about the remaining concepts and elements on the various screens above these are explained in Topics 4.4 and 4.5, which cover Treasury bills, notes, and bonds. The next topic, Trading Treasury Securities, provides an overview of the Treasury markets.