any cases, investors are concerned not only with the value of securities today but also with the value of a position at some time in the future. For example, you may want to know: If I invest $1,000 today at 7% for five years (compounded annually), what will my investment be worth after five years? This is the future value of your investment.

The future value of an investment also provides important "risk management" information. It lets you answer "what if" questions such as: What will be the value of my investment six months from now if spot interest rates increase?

To calculate future values, we continue with the assumption that all spot interest rates are equal. In Chapter 3, you will see how to perform similar calculations with different spot rates for each maturity.

Calculating a future value requires us to replace "discounting" with "compounding." That is, instead of discounting future values to the present, we compound present values to the future. If P0 is the arbitrage-free price relative to the current set of spot interest rates, r, then the future value at time t is:

Computation of this future value actually requires some cash flows to be discounted and some to be compounded, but all aspects are always measured at a common time. To see this, consider Figure 2.3, where we want to determine the value of the bond at the end of Year 1.

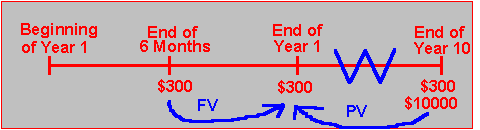
If you want to compute the future value of the coupon bond as of the end of Year 1, you must first compute the future value of the coupon payment at the end of six months, add this to the coupon value as of the end of Year 1, and then add the present value of each of the subsequent coupon payments and the face value. Of course, you neither discount nor compound cash flows occurring at the end of Year 1.

As a result, in Figure 2.3 the future value at the end of Year 1 equals the sum of:

1. The future value of the $300 paid at the end of six months.

2. The $300 paid at the end of Year 1.

3. The present value of an ordinary annuity of $300 per period for 18 six-month periods.

4. The present value of the $10,000 face value paid at the end of Year 10 (18 periods from the end of Year 1).

If the interest rate is 8% per year compounded semiannually, then you can verify that the future value at the end of Year 1 for this ten-year bond is:

$9,349.70 = ($300 x 1.04) + $300 + ($300 x 12.659) + (0.494 x $10,000)

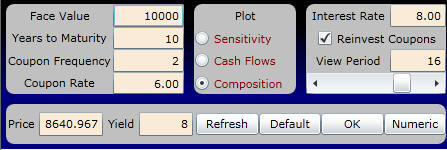
You can use Bond Tutor to verify these figures and step through time using the interactive calculator below.   You can enter the current problem by changing the Interest Rate to 8% and scrolling the View Period to 2, as follows:

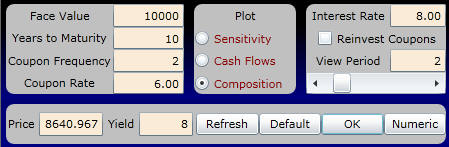
In this form, we have first chosen to consume (i.e., not to reinvest) the realized coupon payments. Equivalently, this is consistent with the perspective of investors in the market at the end of Period 2 (immediately prior to the realization of the current coupon payment). These investors are trading claims to current and future cash flows only.

Online, selecting Composition lets you choose the period you want to view. For the current example, this is one year's time (i.e., View Period 2).

Your display screen appears as follows:

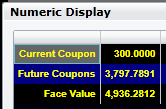
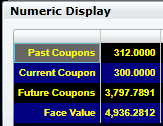
At this point in time, the face value makes up 54.6% of the bond’s value. Numerically, these figures are:

Alternatively, you can repeat the exercise assuming that realized coupon payments are reinvested at the market interest rate. To do this, click on the option Reinvest Coupons in the above interactive calculator.

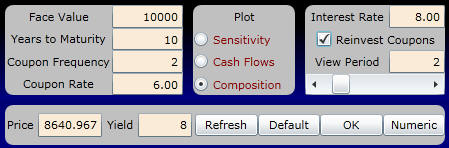
Numerically, this is:

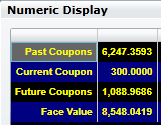
By scrolling the view period, you can take a journey through bond value time. For example, scroll to after 16 periods, above

and verify that the bond value with reinvestment breaks down as follows:

In Chapter 3, The Term Structure of Interest Rates, you will learn how to value fixed-income securities for the case that relaxes the assumption of a constant market interest rate over different time to maturities.