y now, you should understand the concept of yield to maturity. It is the discount rate that satisfies the following equation:

Bond price = Present value of coupon payments + Present value of the face value

The yield to maturity is also known as the internal rate of return on the bond.

Applying this concept to compute the yield on a real-world T-note or T-bond is not an easy task. Complicating factors include:

1. The first coupon period

2. The time of coupon payments and maturity

3. Differences between transaction price and quoted price

4. Accrued interest

5. Other differences, such as notes and bonds targeted to foreign investors

Nonetheless, it is a useful exercise to actually work through a calculation of the yield to maturity on either a note or a bond.

In the following example, apply the skills you have acquired thus far to compute the yield to maturity for a T-note issue, as of April 19, 1994. The details for this note are found in the The Wall Street Journal:

Seven year T-note issued on July 16, 1990, maturing on July 15, 1997.

Coupon rate = 8.5%;

Bid = 106:16; ask = 106.18;

Reported YTM from the ask = 6.23%.

Maturity dates for seven year T-notes are January 15, April 15, July 15, and October 15. For the current issue, the maturity date is July 15. Days to maturity equal 1,182.

Your goal is to verify the reported yield to maturity for this security. You must first calculate the accrued interest before you calculate any yields.

Days from last coupon date = 94

Days to next coupon date = 87

Days between coupon dates = 181

Accrued interest adjustment = +4.25(181 - 87)/181 = 2.207182

Next, let the face value, F, be standardized at 100. Relative to this standard, the current ask price for the bond is 106:18; 106 + 18/32 = 106.5625.

This issue is selling at a premium because its coupon rate at 8.5% is higher than the required rate of return by Treasury investors in the market. As a result, the timeline for cash inflows is as follows:

(Note: The 15 January coupon date is past but is required for computing accrued interest.)

The tricky part is that the current day lies between the two coupon payment dates. Let DC be the days to the next coupon date, which equals 87 days. As a result, the present value of future coupon payments is:

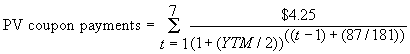
The equation represents the present value of all coupon payments (payable semiannually at (8.5% /2). The added term at the end discounts the present value of the coupon annuity to the current time. It assumes the coupon payment adjustment is made at the time of purchase, so that only the remaining proportion of the coupon payment is actually received.

The remaining term is the present value of the face amount:

Recall that the accrued interest adjustment = $2.2072 (rounded).

At 6.2267%

PV coupon payments = $26.7891

PV face value = $81.9805

Transaction price = $ 108.7696

Less accrued interest adjustment = $2.2072

Quoted price = $ 106.5624

This verifies that the yield to maturity at the ask price equals 6.23%.

The general form for the Yield to Maturity for a T-Note or T-bond is:

where

NC = Number of coupon payments remaining;

C = Coupon amount;

YTM = Yield to maturity;

DC = Days from current date to next coupon date;

DBC = Days between last and next coupon payments; and

FV = Face value

In reality, you cannot earn the yield to maturity you calculate for a T-note or T-bond investment because to do so requires that you reinvest the coupon payments at the security’s yield to maturity. Unless the yield curve is horizontal, the yield to maturity does not exist at a rate at which you can reinvest. Furthermore, the yield curve changes shape over time. This implies that forward rates change, as will the expected future spot rates at which coupon payments are reinvested. The problem of earning the yield to maturity disappears if there are no cash flows to reinvest prior to maturity, as would be the case for zero-coupon bonds.

Using the Treasury Calculator

Online, you can work this example using the Treasury Calculator. Access the Treasury Calculator by choosing the Treasury Calculator from the Subject menu.

Online, you can verify that the day count data, required for accrued interest, is entered as:

Days from last coupon date = 94

Days to next coupon date = 87

Coupon rate = 8.5%

Quoted price (to buy from) = 106.18

Tick size = 32nds

Suppose you want to calculate the cost of acquiring a claim to $1,000,000 face value for this security. Enter $1,000,000 for the face value and click on the OK button for Bonds and Notes:

By using the online interactive calculator you can verify that the cost of acquiring $1,000,000 face value, taking into account accrued interest, is $1,087,697.00, and the yield to maturity is 6.23.