n active strip market is useful for a number of reasons. First, it is in the correct form (i.e., zero-coupon bonds with approximately zero default risk) for plotting the yield curve. Second, it provides a means of hedging interest rate risk in the form of synthetic equivalents of the position to be hedged. For example, a portfolio of strips can be formed to replicate exactly the coupon note or bond that is stripped. If any pricing discrepancies exist, it is possible to construct an arbitrage-based trading strategy designed to exploit small differences.

What would happen if the value of a portfolio of strips were higher than the coupon bond itself? Clearly, if this were the case, you would want to buy low (the coupon bond) and simultaneously short sell the portfolio of strips. This would lock in an arbitrage profit. Registered dealers have a transaction cost advantage for engaging in this type of trading exercise. They can either trade directly in the secondary markets, or enter the market, buy the coupon bond, strip it and resell it to the strip market for an arbitrage gain. As a result, we would expect prices in the strip markets and the market for T-notes and T-bonds to converge.

If the stripped components are worth more than the whole, because of investor preferences, the existence of arbitrage opportunities between the two markets implies that the T-notes or T-bonds should be bid up at the Treasury auction to equal their stripped value. That is, the Treasury benefits without actually having to issue strips. It is not surprising, therefore, that the Treasury now sanctions trading in strips.

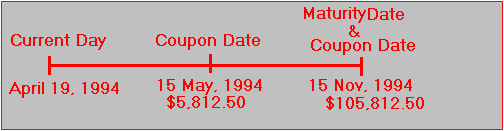
Using the example in Topic 4.7, we can check the values between the strip and the Treasury-note markets.

Consider a portfolio of 58.125 May 94 ci strips, 58.125 Nov 94 ci strips, and 1,000 Nov 94 np strips relative to a face value of $100. This portfolio provides the following cash flows:

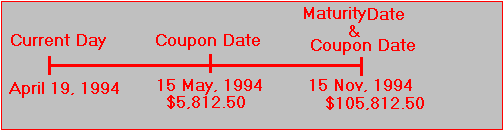
Now consider T-notes (11 5/8% maturing on November 15, 1994) with a maturity value equal to $100,000:

The two portfolios provide identical cash flows.

On the Treasury note market, the second portfolio has a bid and ask equal to: 103:29 103:31 (decimal bid/ask prices equal 103.9062, 103.9687).

That is, you can buy from the ask the $100,000 maturity value T-note for $103,968.75 and sell the $100,000 maturity value T-note for $103,906.20. The difference is the dealer’s spread.

Recall that quoted prices for T-notes on the secondary market do not reflect the accrued interest on the security. The buyer must pay the seller an additional amount to compensate for accrued interest. For the current example, we can compute the accrued interest as follows:

Days from last coupon date = 154

Days to next coupon date = 26

Days between coupon dates = 180

Let the face value be standardized at 100. The accrued interest adjustment is +5.8125(154/180) = 4.9729

If you engineer the T-note in the strip market from its stripped components, then the prices are:

This will cost:

58.125(99.75)+1058.125(97.5) = $108,965.20

To sell will generate revenue equal to:

58.125(99.75)+1058.125(97.46875)= $108,932.10.

To purchase the note directly will cost $103,968.75 + $4,972.90 = $108,941.65,

and to sell will generate revenue equal to $103,906.25 + $4,972.90 = $108,879.15.

Note that the prices between the two markets are strikingly similar, which indicates that, for this issue, there is no arbitrage opportunity.

Note on Constructing Your Own Yield Curve

If you assume that no arbitrage opportunity exists between the strip and the other Treasury markets, you should construct the yield curve directly from the strip market. This is simple and eliminates any problems associated with progressive calculations using T-notes and bonds as well as knowing the precise contractual details for these securities.