t the close of markets for Friday, September 16, 1994, the following data was recorded on the T-bill futures for June delivery.

Similarly, on the same day, the closing information for 12-month T-bills maturing on June 29, and September 21, 1995, was:

(Source: Investor’s Business Daily, Monday, September 19, 1994)

The settlement date for the futures contract is June 22, 1995. The price of the futures contract is:

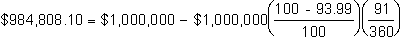
The implied yield to maturity (compounded anually) from this contract is:

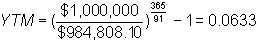
Furthermore, on this day the spot rate for the closest T-bill maturing around June 22, 1995, had a bond equivalent (ask) yield equal to 5.50%, (the closest being the June 29, 1995 contract). In order to compare different yields from the same frame of reference, we first compute the yield to maturity, compounding daily, for this T-bill. Online, using the calculator in Bond Tutor, you can verify that this is 5.44%:

In the online calculator select the Treasury Bill tab and enter the following:

In the bottom date calculator enter 9/17/1994 for Today and 6/29/1995 for Future date or just enter 285 days directly and then enter 5.25 for the Discount Yield.  Click calculate to verify the yield to maturity is 5.437%.

Now, by working in period sizes of one day, the implied spot rate for September 21, 1995, is:

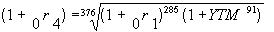
Let the YTM be converted into a daily rate (0.0633/365), and the spot rate be converted into a daily rate (0.0544/365). Then,

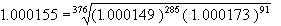
Annualized, this spot rate equals 5.66%.

The spot bond equivalent yield for the September 21, 1995, T-bill is 5.79%. To be comparable, we first convert this into a yield to maturity compounded as follows:

Online above now enter the date September 21, 1995 for future date and 5.79 for discount yield to verify the Yield to Maturity equals 5.708% which is quite close to the implied spot rate of 5.66%, using the T-bill Future’s price.

The implied repo rate is the interest rate earned by someone who buys the underlying T-bill and simultaneously sells the future. (The term repo refers to "repurchase".) This strategy is shown on the following timeline:

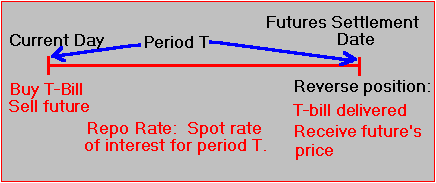
In this transaction, the life of the T-bill must equal the sum of the period of time until the future's settlement date plus the maturity of the T-bill delivered. With this strategy, you are holding one T-bill for a shorter time than its actual time to maturity. By selling the future, you have locked into a price for selling your T-bill at the time of settlement for the future's contract.

In effect, you have constructed a synthetic T-bill for the period of time from the present until the futures settlement date. Presumably, the interest you earn from this strategy is very close to what you would earn if you bought a T-bill with this shorter maturity. In the absence of marking to market, it should be exactly the same.

Alternatively, you can look at repo rates from the perspective of being a cost of carry. In this interpretation, you are an investor who wants to compare the difference between the cost of buying and holding the underlying security versus buying the T-bill future. That is, to acquire the underlying T-bill, you can:

i) Purchase the T-bill directly with time until maturity equal to m+n days.

ii) Purchase the T-bill future and hold it until its maturity in m-days time, at which time the seller delivers to you a T-bill with life equal to n days.

At the time of the future’s maturity, you must be indifferent between i) and ii), since the futures price on that date will equal the price of the underlying T-bill. Ignoring the effects of marking to market, the only difference between these two alternatives is the cost of carrying the T-bill for m days, where m is the number of days between the time of settlement and the present time now.

In the absence of arbitrage these two alternatives are the same when adjusted for the cost of carrying the underlying T-bill for this time. As a result, the cost of carry is the difference between the futures price and the spot price, and thus the implied repo rate return can then be computed as the spot rate of interest for carrying the underlying T-bill for m days.

We will now compute the implied repo rate for the T-bill futures example introduced earlier in this topic.

Recall that the price of the futures contract settled on June 22, 1995, is:

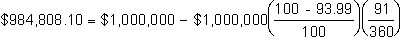
and the discount for the $1,000,000 September 21, 1995, T-bill contract, using the ask price, is:

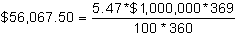
Therefore, the contract value for the September 21, 1995, T-bill is:

$1,000,000 - $56,067.50 = $943,932.50

The difference between the futures price and the underlying T-bill spot price is the cost of carry, which equals:

$984,808.10 - $943,932.50 = $40,875.60.

Now, recall that the spot rate of interest for the closest T-bill to settlement had a bond equivalent yield equal to 5.50%. Earlier in this topic, this was converted into a yield to maturity which equaled 5.4371% (compounded daily). Therefore, the future value of $943,932.50 at 5.4371% for 285 days (compounded daily) is:

$984,865.98

The two figures ($984,808.10 for the futures price and $984,865.98 for holding the T-bill) are strikingly similar. Although it is slightly cheaper to purchase the September 21, 1995, T-bill via futures than to purchase the September 21, 1995, T-bill directly, the former is marked to market on a daily basis. Effectively, the repo rate, even allowing for marking to market, is approximately the same as the spot rate of interest computed from the Treasury market for this same period of time.

In the next topic, T-Note and T-Bond Futures we consider these important types of derivative securities.