he most active Treasury futures are the Treasury bond and Treasury note futures traded at the Chicago Board of Trade. Both futures contracts trade in units of $100,000 and expire in May, June, September, and December.

One measure of activity in these contracts is called "open interest." This is the number of contracts outstanding. For example, at the close of trading on Friday, September 16, 1994, the reported open interest for Treasury bond futures was 264,993. The open interest for T-note futures was 269,745 and 188,736 for the 10- and 5-year notes, respectively. At this same time, there were 17,238 contracts outstanding for T-bill futures.

The quoted price for a T-bond or T-note future is the same as the price for T-bonds and T-notes (which is different from T-bill futures). The quoted price is given in thirty-seconds not - decimals. For example, at the close of markets for Friday, September 16, 1994 ¾ the following data was recorded on the U.S. Treasury bond futures December contract:

(Source: Investor’s Business Daily, Monday, September 19, 1994)

The bid and the ask are given relative to a standard face amount of $100; the contract size is $100,000. Thus, the contract value at the close price of 99-8 is:

The last trading day is the 7th business day preceding the last business day of the delivery month and delivery is via the Federal Reserve's book entry system. Both of these future contracts are settled for script (respectively, T-bonds for T-bond futures and T-notes for T-note futures), not cash. The settlement procedure, however, is rather complex because there exists a range of acceptable securities and options that the short side of the market can exercise.

In general, futures contracts often provide the short side with options as to what, when, where, and how much is delivered. These options are known as delivery options, and their presence complicates the pricing problems for futures contracts. Treasury note and bond futures are no exceptions. They provide the short with a set of delivery options over when and what is delivered. We will discuss these options next.

T-bond futures can be settled with any T-bond that has 15 or more years to first call or maturity (whichever comes first). To add to the settlement complexity, this flexibility is combined with a number of settlement options that the seller of the future can choose to exercise. In this section, the settlement procedure is described in general. Readers interested in the exact contractual details should contact the exchange.

In order to get an overview of the settlement procedure, consider the following timeline:

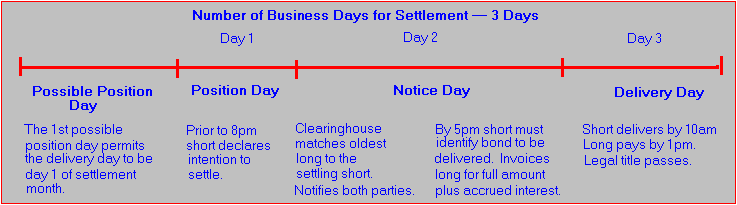
The first possible position day can be fixed, at the earliest, two business days in the month prior to settlement so that the first possible delivery day is Day 1 of the settlement month. However, the rules for delivery give the seller a set of delivery options.

The first option represented on the timeline is the "timing option." This option gives the short the right to choose which business day of the settlement month is to be designated as the delivery day (Day 3 on the timeline above).

A second pair of options, with short duration, are as follows. First is the option to notify the position day up to 8 p.m. ¾ that is, 6 hours after the close of futures trading. Second is the option to choose which bond is to be delivered by 5 p.m. on the business day after the position day is also fixed.

This decision is not straightforward (although the rules can be automated on a computer program). For settlement of a Treasury-bond future, recall that any U.S. T-bonds that are not callable for at least 15 years and have a maturity date of 15 years or more from the first day of the delivery month are acceptable.

Given the range of bonds that can be delivered, the short calculates the "cheapest to deliver" bond. The problem facing the short is to deliver T-notes or T-bonds that cost the least amount to acquire but have the largest invoice amount. The invoice amount is the amount that the long must pay the short when the underlying security is delivered. Details of its computation are described next.

Calculation of the invoice amount is straightforward once you understand "conversion factors." Conversion factors arise because there are bonds with different coupon rates that can be delivered. Initially, all quotes are for a bond with a coupon of 8%. A bond with a different coupon is "converted" into an 8% bond by multiplying its price with a conversion factor. These factors are published by the CBOT.

Given the conversion factor, the invoice amount is calculated as follows:

where DQP is the decimal value of the settlement price and Accrued interest is that on the underlying bond at the delivery date.

What happens with the conversion factors is that they are based on the assumption of a flat term structure. In practice, the term structure is almost never flat, and thus the shape of the term structure, combined with the fixed conversion table, implies that some bonds are cheaper to deliver than others.

Recall, however, the sequence of events required for delivery, which last for three business days. The short must first declare a position day and then declare the security that will be delivered on Day 2. Actual delivery takes place on Day 3. As a result, this settlement profit/loss is not riskless and so a positive value does not necessarily imply an arbitrage opportunity to the trader who is selling in the settlement month.

A second way to see which bond to deliver is to compute the implied repo rate. You saw implied repo rates in the T-bill futures topic. It is the yield to maturity that is earned by simultaneously buying the deliverable and selling the future.

The difference between the price of a T-bond or T-note future and the spot price (adjusted by the relevant conversion factor) on the cheapest to deliver underlying T-bond or T-note, converted to an annualized rate, is called the implied repo rate. You may recall from the T-bill future’s topic that this is the implied cost of carrying the underlying Treasury over the period of time from the time of purchase to the time of the future’s maturity.

You also know that (ignoring the effects of marking to market on the price of a future), you can view the implied repo rate as the spot rate of interest earned from creating a synthetic T-bill. Here, this is formed by simultaneously buying the underlying T-bond or T-note and selling the future. This synthetic position is reversed at the time of the future’s maturity, which is equivalent to a synthetic bond with a time to maturity that depends on the life of the futures contract, DM. This is illustrated in Figure 5.4.

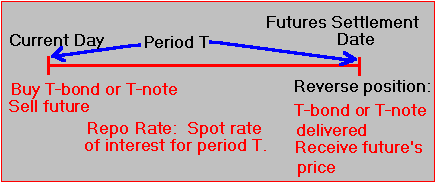
The repo rate is the yield to maturity earned from this synthetic contract. The annualized repo rate can be computed as follows (assuming no coupon payments between the present time t and the time of the future’s maturity):

where:

DD = Delivery day,

DM = Days to the maturity of the future,

DQP = Decimal value of the future’s price,

Accrued Interest, AI, is at the time of the delivery date when subscripted by DD and the present time when subscripted by t.

If coupon payments are made by the underlying security between the present time and the time of the future’s maturity, then an additional term is added to the numerator of the repo rate equation. This term is the future value (at the time of the future’s maturity) of all interim coupon payments.

It is useful to compute the repo rate because the cheapest T-bond or T-note to deliver will be the one with the highest implied repo rate. But we would expect the maximum implied repo rate for Treasury bond and note futures to be less than both the spot rate implied from the yield curve and the implied repo rate for Treasury-bill futures defined over the same time period. This is because there is an implied set of delivery options associated with the way Treasury-bond and note futures are settled. Because it is the short side that acquires these options, arbitrage-free pricing implies that this side cannot acquire these options for nothing. Instead, the value of the option will be reflected in the reduced price of a future that the short side receives.

In the next topic, Valuation of T-Note and T-Bond Futures, under the assumption that the futures price equals the forward price, the arbitrage-free price of the future is derived in the presence of one such option, the quality option.