5.6 Euro-Markets
These markets consist of demand deposits located in major banks outside of the country whose currency is used for the deposit. For example, Eurodollars are U.S. dollar-denominated demand deposits located in major banks outside of the U.S. Similarly, Euroyen, Euromark, Eurosterling and so on, are denominated in their respective currency but deposited outside of their respective countries.
The globalization of financial markets, combined with strict regulatory requirements within countries for their own currency, has created tremendous growth in the Euromarkets. These markets combine the currency of one country with the banking regulations of another country. As a result, this liquid market can adapt very quickly to undo strict regulation in any country.
Trades take place in a noncentralized market structure, largely by a network of dealers linked by telephone. This provides an extremely liquid money market for large corporate and financial institutions.
Eurodollars are distinct from dollar Eurobonds in that the former are offshore deposits whereas the latter are dollar-denominated, offshore "bearer bonds." For the latter, no record is kept and evidence of ownership is physical possession. Interest is tax-free, or adjusted sufficiently to allow for any withholding tax, so that to the owner, it is tax-free. Eurobonds are only issued by very low credit risk institutions and are underwritten by major banks.
Euro Quotations
Rates for offshore deposits are quoted by each dealer for a range of maturities. Table 5.1 provides the LIBOR-offered eurodollar rates for some major dealers as of 10:00 GMT on Eurodollar deposits by maturity on Monday June 27, 1994 (Source: FAST Trading Room, Carnegie Mellon University).
Table 5.1 Rates for Eurodollar Deposits
|
Period |
Barclays |
Bank of Tokyo |
Bankers Trust |
NatWest |
|
Week |
4-5/16 |
4-3/8 |
4-5/16 |
4-5/16 |
|
1 Month |
4-1/2 |
4-1/2 |
4-7/16 |
4-1/2 |
|
2 Month |
4-5/8 |
4-5/8 |
4-5/8 |
4-5/8 |
|
3 Month |
4-3/4 |
4-3/4 |
4-3/4 |
4-3/4 |
|
6 Month |
5-1/16 |
5-1/16 |
5-1/16 |
5-1/16 |
|
9 Month |
5-1/2 |
5-1/2 |
5-1/2 |
5-1/2 |
|
12 Month |
5-3/4 |
5-3/4 |
5-3/4 |
5-3/4 |
Interest on Eurodollar deposits is quoted as simple interest, in fractional form, and is applied on an add-on basis. In applying these rates, a year is assumed to be 360 days and days are actual. Therefore, interest on a $100-dollar 3-month deposit with an actual day count equal to 91 days, and a Eurorate of 4-3/4% per annum is:
![]()
The rate of interest on Eurodollar deposits among major international banks is generally referred to as the London Interbank Offered Rate (LIBOR) (with the exception of the French franc and the Hong Kong dollar see table 5.2). Although LIBOR is applied on a simple add-on basis, the day count convention for applying LIBOR can vary among the major currencies. Table 5.2 provides a summary of these daycounts for a sample of currencies.
Table 5.2 Daycount Conventions for the Euro-Markets
|
Interbank Offered Rate: Currency |
Day Count Convention |
|
Deutschmark LIBOR |
Actual/360 |
|
Dollar (Australia) LIBOR |
Actual/360 |
|
Dollar (Canada) LIBOR |
Actual/360 |
|
Dollar (Hong Kong) HIBOR |
Actual/360 |
|
Dollar (N.Z.) LIBOR |
Actual/360 |
|
Dollar (U.S.) LIBOR |
Actual/360 |
|
ECU LIBOR |
Actual/360 |
|
Franc (French) PIBOR |
Actual/360 |
|
Franc (Swiss) LIBOR |
Actual/360 |
|
Japanese Yen LIBOR |
Actual/360 |
|
Lira LIBOR |
Actual/360 |
|
Sterling LIBOR |
Actual/365 |
It is an important interest rate that can be traded indirectly in different ways. Some contracts are traded directly in terms of yields. For example, a division of the Chicago Mercantile Exchange, called the International Monetary Market (IMM), trades cash-settled futures on Eurodollar yields. Settlement and marking to market are completed using a sampled spot-LIBOR rate. The clearinghouse for the futures market determines each day LIBOR from a random sample of 12 major banks selected from a set of at least 20 banks. Banks are selected at two periods of time --- the close of the futures market and some time within 90 minutes of the close. At the time of selection each bank provides an annualized quote for a three-month Eurodollar deposit. To estimate LIBOR at a point in time four quotes are dropped, the highest and lowest two, and LIBOR is computed as the arithmetric average of the remaining quotes.
The Term Structure of LIBOR Rates
At the end of each day, the LIBOR page provides LIBOR rates for different maturities for Eurodollars, Euroyen, Euromarks, etc. That is, the short end of the yield curve can be plotted directly for each Eurocurrency. In practice, this is an important yield curve that is used for pricing a range of securities. Its importance arises because the Euromarkets are extremely liquid and can be used in the construction of hedges (in the form of a synthetic equivalent form of a security), which are required for the arbitrage pricing of a wide range of different financial contracts. The cost of the synthetic equivalent establishes a zero-arbitrage bound on a security's value.
As a result, different shapes of the Euroyield curve contain important information. In particular, implied forward rates can be extracted and interpreted using the various theories of the term structure of interest rates. For example, an upward sloping curve under the expectations theory implies that the increasing implied forward rates are unbiased expectations of expected future spot rates.
LIBOR traders can lock into the implied forward rates by trading derivatives such as Eurodollar futures and forward rate agreements (FRA). You can work through the operational details of these arrangements in the next section.
The Use of Forward Rate Agreements
Forward rate agreements (FRA) are agreements that allow forward rates to be traded for standard Eurodollar maturities (3 month, 6 month and 12 month deposits). For example, a "three-against-six" FRA is structured to commence at the time of maturity of a new 3 month Eurodollar deposit and end 3 months (using actual day counts) after this commencement date (i.e., 6 months from now). This three-against-six contract fixes some rate now, fr, and is cash settled using the difference between fr and the realized 3 month spot rate for LIBOR in 3 months’ time. A year for a FRA can be either 360 days or 365 days and is specified in the contract.
If the realized spot LIBOR rate is higher than fr, then the buyer of the contract gains and receives, in cash, the present value of the increased interest expense on the nominal value of the contract. If the spot rate falls, then the seller gains, because the buyer must compensate the seller for the present value of the difference between the agreed-upon rate and the realized spot rate times the nominal value of the FRA. All discounting is at the realized spot rate.
That is, for a "M against M+DM" FRA, the seller pays the buyer an amount equal to:
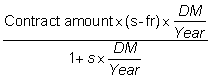
where
Contract amount = Nominal value of the FRA,
DM = Number of days in the FRA,
S = Spot rate for the maturity of the underlying Eurodollar deposit that is realized at the time of maturity,
fr = Agreed-upon forward rate, and
Year = Either 360 or 365 days, as specified by the contract.
That is, the FRA is settled at the end of M days for the present value, using s and time DM, for the interest expense differential between the realized spot rate, s, and the agreed-upon forward rate, fr.
The timeline for this FRA is represented in Figure 5.5:
Figure 5.5 Timeline for a Forward Rate Agreement
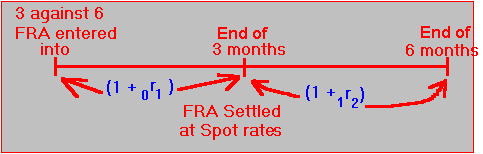
At the time of entering into a three-against-six FRA, both the 3 month and the 6 month spot LIBOR rates are known. From these rates, the implied 3 month forward rate,
1r2, can be calculated.Example: Implied Forward LIBOR Rate
In this example, we apply the information contained in Table 5.1 to compute the implied 3 month forward rate. It is computed using the 3 month and 6 month spot rates, 4- 3/4% (4.75%) and 5-1/16% (5.0625%), respectively.
Recall from the topic forward interest ratesfir_tsr, in Chapter 3, that the annualized forward 3-month rate, 1+
1r2, is computed from the two spot rates as follows: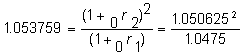
FRA Rates versus Implied LIBOR Forward Rates
The M-against-M+DM FRA is settled at the end of M-days for the present value of the interest expense differential between the realized DM-days LIBOR spot rate s, for the DM-days covered by the FRA, and the agreed upon forward rate, fr, in the FRA. This rate must equal the implied forward LIBOR rate,
1r2, at the time of entering into the FRA. If this is not the case, an arbitrage opportunity is created, because by using FRAs and Eurodollar deposits, you can lock into the implied forward rate in the LIBOR curve with certainty and therefore exploit any under- or overpricing of the FRA by going long or short as required.Locking in Forward Rates
To see how the rate is locked in, consider the case where the FRA rate, fr, equals the implied forward rate. Suppose you take a position that is long the three-against-six FRA and long Eurodollars at the 6 month rate. This locks in the implied 3 month forward rate in the 6 month Eurodollar deposit. At first glance, it may appear unusual that both positions are long in this hedge, but recall that the present value of a deposit and interest rates move in opposite directions.
To see how the hedge works, consider what happens under the following alternative LIBOR realizations. First, suppose that the implied 3 month forward LIBOR rate is realized. The FRA is settled with a zero net-cash transfer and your long 6 month Eurodollar position earns the original forward rate. This, by assumption, is the realized spot rate for the last 3 month period. Second, suppose that the realized spot rate does not equal the original implied forward LIBOR rate. For this case, we consider the changes in value of the two components of your position:
A. Let the realized spot rate be higher. The market value of your long Eurodollar deposit declines but you receive a positive net-cash difference from your long FRA position.
B. Let the realized spot rate be lower. The market value of your long Eurodollar deposit increases but you pay the net-cash difference on your long FRA position.
As a result, for both A. and B., the two components move in opposite directions, which, if appropriately weighted, exactly offset each other.
Example
To see this numerically, suppose at time t
0 you deposit $1,000,000 for 6 months at 5.0625% annualized and go long a three-against-six FRA with a nominal value that equals [$1,000,000*1.050625*182/360]/[1+.053759*(91/360)] = $1,011,843.72. Let the day count for one year be 360 and note that interest is computed on an add-on basis.Case I
For this case assume that at time t
0 + 91 days, the realized spot rate equals the implied forward rate of 5.3759%.At time t0 + 91, your $1M deposit is worth:
$1,000,000*[1 + (0.050625*182/360)]/[1+ (0.053759*91/360)] = $1,011,843.72
The FRA is cash settled at 0 and, therefore, you earn the implied forward rate for the time period t0 + 91 to t0 + 182 on your $1,011,843.72 investment value at time t0 + 91.
Case II
For this case, assume that the realized spot rate is higher and equals 5.5%.
At time t0 + 91, your original $1,000,000 deposit is worth:
$1,000,000*[1+(0.050625*182/360)]/[1+(0.055*91/360)]=$1,011,530.66
The FRA is cash settled for the present value of the net interest difference, which equals:
$1,011,843.72*(0.055-0.053759)*(91/360)/(1+0.055*91/360)=$313.06
Summing the two values ($1,011,530.66 + $313.06), $1,011,843.72 is the total value for Case I at time t0 + 91.
That is, as the realized spot rate increased, you lost money on the value of your two period investment but gained an equal amount from your FRA. Therefore, again you earn the implied forward rate on your $1,011,843.72 investment at time t0 + 91, because this is locked into the original 6 month spot rate. Therefore, the terminal value for Cases I and II are identical.
In summary, the FRA allows two banks or other institutions to lock in the implied forward rate, in a LIBOR yield curve. In this case, interest is computed on a simple "add-on" interest basis, using either a 360 or a 365 day year and counting the days to maturity in the period of time covered by the forward rate agreement.
In the next topic, Eurodollar Futures we introduce this important market.
 office (412)
9679367
office (412)
9679367