uppose you have the opportunity to invest $100 for one year at 10% interest. At the end of the year, your investment is worth $110: the $100 you invested plus (0.1)(100) interest:

$110 = $100(1 + 0.10)

Here, $110 is called the future value of $100 invested at 10% today.

Now, what is the value today of $110 in one year? The answer is called the present value of $110 in one year discounted at 10%. It is calculated by rearranging the future value equation:

Next, ask the following question: If the present value of $110 in one year is $100, what is the interest rate? The answer, of course, is 10%, again calculated by rearranging the future value equation:

To describe these valuation principles more generally, let FV = future value, PV = present value, and r = interest rate. Then, the relationship among these variables is:

Therefore, if you know the future value (FV) and the interest rate (r), you can calculate the present value (PV). Similarly, you can calculate the future value from the present value and the interest rate, or the interest rate from the other two variables.

A Two-Period Example

Now, suppose an investment opportunity will pay you $121 at the end of two years. What is the value today (i.e., the present value) of this opportunity?

To work out the answer, we work backward by solving two one-period problems.

First, suppose you are at the end of Year 1. What is the value of $121 in one year? As you know, the answer depends on the interest rate between Year 1 and Year 2. If this is 10%, then the value at the end of Year 1 is

Second, what is the value today of $110 in one year? You already know that the answer is $100:

Note that you have to discount the $121 twice, once for each period. If the interest rate is r per year, then the relationship between the future value and the present value is

You can easily deduce the general principle. If the interest rate is r per year, and you receive FV in t years, then the present value is

An example of a fixed-income security that has only one future payment is a zero-coupon bond. You will encounter these in much more detail throughout this text.

A Three-Period Example

In the two-period example, you started with the future value and worked back to the present value. You can also start with the present value and work forward.

Suppose you can invest $100 for three years at 10% per year. This means that each year, you will earn 10% on whatever you invest that year. You already know that your $100 will be worth $110 in one year. If you reinvest the $110 at the end of the year, the value at the end of Year 2 will be $110(1 + 0.10) = $121. Equivalently, this equals:

If you reinvest the $121, then at the end of Year 3 you will have:

The value of your investment over time is shown in Figure 1.1.

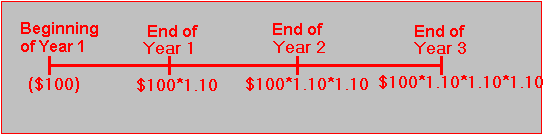
The relationship between present and future values in this example can be summarized by noting that as an investor, you are indifferent among:

1. $100 now,

2. $110 in one year’s time,

3. $121 in two years’ time, or

4. $133.10 in three years’ time.

We state this as:

More generally, if you invest PV now at interest rate r per year, then the value at the end of year t is

A Sequence of Cash Flows: A Two-Period Example

So far, we have valued single payments in the future. We now examine a sequence of future payments. Suppose there is an investment opportunity that pays $50 at the end of Year 1 and $100 at the end of Year 2. If the interest rate is 8%, what is the present value of the future cash flows from the investment?

The answer is obtained by discounting each part separately and then adding present values, a principle known as value additivity:

The important point to remember is that money received at different times cannot be added together; a dollar today is very different from a dollar to be received one year later. However, you can add present values together, as we have done. In fact, you can add the value of dollars together whenever they are expressed with respect to any common time, present or future.

When the price of a fixed-income security is determined in the market, investors are in this same position; they are valuing cash flows that occur at different times. From value additivity, the price of the security is the sum of the present values of the future cash flows.

Given the price at which investors buy or sell a security, we can ask the question: What is the interest rate that investors are implicitly using to discount cash flows?

In our current example, suppose that the market price is $138.32. You can calculate the implied interest rate, r, from the following:

You can verify that r = 0.05, which is the rate that equates the present value to the sum of the discounted future cash flows.

In the next two topics, we apply time value of money concepts to value two types of fixed-income securities: annuities and bonds.