The following story was reported by The Pittsburgh Press Wednesday, June 14, 1989.

Willa T. shared in the Lotto jackpot on February 10, 1986. She won $454,389.63. At first she found winning thrilling, but at her age, she found that "the thrill wears off when the prize comes in 21 installments."

Mrs. T. was entitled to receive $21,638.03, or $17,310.43 after federal withholding tax. After collecting four installments, Mrs. T. decided to sell her remaining 17 installments for an immediate payment of $111,000.

Mrs. T. hired an attorney to sell the remaining installments. At a dinner party, the attorney ran into the financial consultant. The financial consultant was reported to have said that buying the annuity "fits right into my portfolio."

How do you think each of the parties fared in this transaction? The answer to this depends upon how you would value Mrs. T.'s lotto annuity.

We will now apply Bond Tutor to work through this example. First we make several simplifying assumptions:

Taxes: For incremental cash income less than $30,000 per year, let the assumed tax rate be 20%. For incremental cash income greater than $100,000 let the tax rate be 35%.

Market Information: At the time of this story, the yield to maturity on a long-term Government bond was 8.40%.

Annuity Assumption: Remaining annuity is an ordinary annuity from the present time of June 14, 1989.

Mrs. T.'s annuity of $21,638.03 for 17 years is virtually a riskless sequence of cash flows. The state of Pennsylvania has invested in a trust account an endowment to cover cash payments. As a result, in a perfect market, with no taxes, transaction costs, or liquidity problems, Mrs. T. would receive the present value discounted at 8.40 using interest rates in 1989.

Online in the calculator below set up the problem as follows.

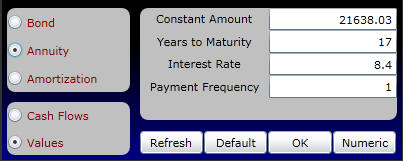
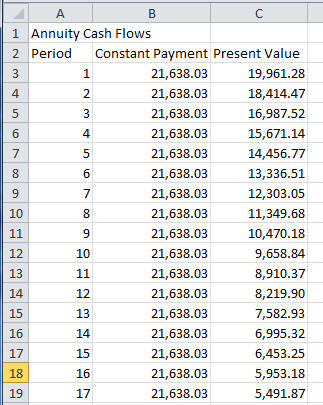
The annuity value of the remaining 17 payments, measured in both nominal and present values, declines over time as follows:

Numerically this equals where the undiscounted value in period 1 equals $21,638.03*17=$367846.51.  Online click on the Numeric button to see the undiscounted and discounted values per year.

Thus, in a perfect market the present value is $192,216.20 when discounted at 8.40% compounded annually.

Unfortunately, Mrs. T. faces several types of market imperfections: taxes, no organized market for Lotto payments, and legal fees.

Ignoring legal fees, Mrs. T. received $111,000 from the financial analyst. Now suppose Mrs. T. pays 35% in tax. This leaves $72,150 -- and even less after legal fees.

As a result, Mrs. T. has lost a lot due to market imperfections.

With your acquired knowledge from Chapter 1 to date about the time value of money, can you improve on the reported result?

The attorney was quoted as saying that he first contacted several financial institutions. These institutions were not interested because the prize was not large enough. However, by framing the question in terms of the bank's regular business, the following deal could potentially be struck.

Mrs. T. takes out a standard 5-year personal loan for $62,400. In return, Mrs. T. assigns (recall that the courts approved the sale) the after-tax lotto revenues ($17,310.42) to the bank for 5 years. Structuring the settlement this way requires no additional cash outlay by Mrs. T. and lets Mrs. T. keep the lotto annuity for Years 6 - 17. She could repeat the transaction on February 10, 1994.

At the time of the article, the personal loan rate was 12%. The bank is strictly better off with this loan because the cash flows are riskless, whereas personal loans are risky. As a result, a better-than 12% rate should be negotiated by Mrs. T.

If the bank booked a 6-year personal loan at 12%, then Mrs. T. could borrow $71,170.19 in the same way. This amount approximately equals her after-tax settlement, but once again, Mrs. T. can repeat the transaction on February, 10, 1995!

In fact, Mrs. T. would have received $138,856.50 if the bank had booked a 17-year loan at 10%. The bank is strictly better off in this case because the repayments have zero default risk and at the time of the article, the 17-year Government bond rate was 8.40%. Mrs. T. is clearly better off she receives $138,856.50 now and faces no future liabilities. That is, her loan repayments are covered by assigning the after-tax Lotto receipts to the bank.

In the solution reported by the newspaper, an arbitrage opportunity exists. That is, an opportunity exists for an investor with zero cash outlay to generate strictly positive cash flows.

Suppose some outside party had sufficient equity in his/her home or other real estate to take out either a first or second mortgage to cover the $111,000. At the reported settled amounts, a pure arbitrage opportunity exists by paying Mrs. T. $111,000 for the Lotto annuity.

To see why, suppose the third party buys the Lotto annuity from Mrs. T. and finances this investment by borrowing the entire amount of $111,000 against some property. Assume that the mortgage loan is booked at a fixed rate equal to 10%.

Online, we can work out the arbitrage opportunity.

The first part of the problem is to compute the cash outflows from borrowing $111,000 over a ten-year period at 10%. To simplify the problem, assume that all cash payments are annual.

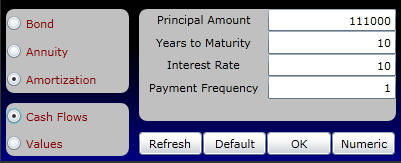
Click on Amortization and Cash Flows as follows:

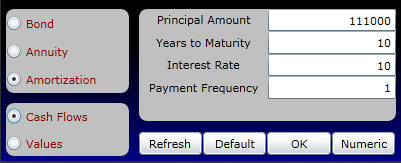
Online enter the above numbers and click on OK.  Then click on the Numeric button and you will see for this mortgage loan the cash repayments as well as the part of these repayments that service the interest expense:

You can open a spreadsheet and cut and paste these numbers from Bond Tutor in order to complete this analysis.

That is, from the Lotto payments calculator at the beginning of this section, click on the Numeric button to get the Lotto unity payments and then copy the data.

Second, open your spreadsheet and paste in the raw Lotto numbers:

Again from the popup grid containing the numbers for Constant Payment and Interest Expense.  Copy and then paste into cell D1 in the above spreadsheet.

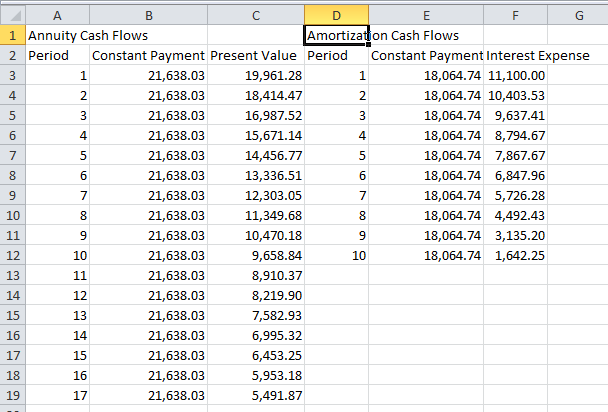
Now the above cash flows can be matched to illustrate the arbitrage:

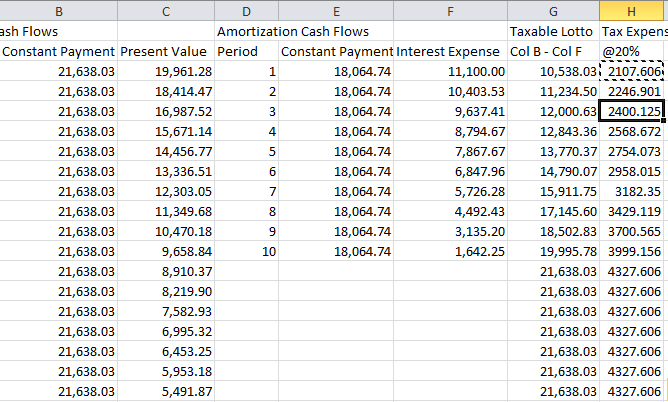
First, the interest expense on the mortgage loan is tax deductible and serves to reduce the Lotto receipts.  In the spreadsheet below the taxable lotto payments are in column G (Column B - Column F) and the cash tax expense equals the numbers in column H.  This is illustrated below:

Finally we need to account for the cash Mortgage repayments which are in the above spreadsheet in Column E.  Thus the after tax cash flows can be calculated as follows in Column I as Col B - Col E - Col H:

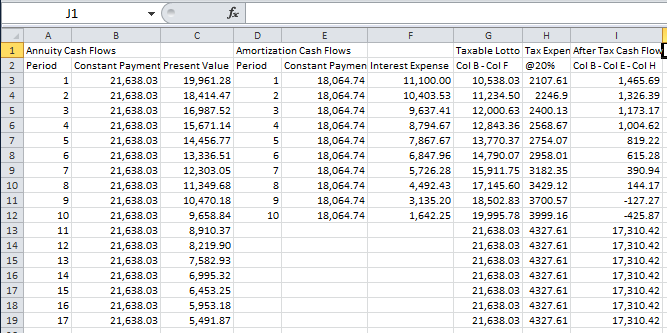
The pure arbitrage opportunity is revealed from the realized net positive cash flows in every year except Years 9 and 10 in Column G. The positive cash flows from earlier years easily eliminate these two negative years.

This Lotto case illustrates that with zero cash outlay, a strictly positive return is earned. This is an arbitrage opportunity. Clearly, the arbitrage-free value of the Lotto winnings is significantly higher than what Mrs. T. received.

In Chapter 2, we further develop the no-arbitrage arguments to the problem of valuing bonds.