o, we have seen that cash matching controls the exposure of a position to shifts in the yield curve by matching the position's cash flows synthetically. That is, if n cash flows are realized over time, then the cash-matching approach requires that all n dimensions be managed. In contrast the approach developed in this topic requires only one measurement to be considered: the position's duration.

A Simplified Approach to Hedging Interest Rate Risk

Before formally developing the concept of duration, let us first examine how interest rate risk affects the value of some fixed-interest security, such as a bond. Recall that the present value of a bond is given by

where C is the cash flow at time t and r is the internal rate of return of the bond.

The concept of duration was first introduced by Macaulay. It measures the interest rate sensitivity of a bond's value and is derived as follows.

Let r be a bond’s yield to maturity, so that r solves

where C is the coupon payment, F is the face value, T is the maturity of the bond, and P is the current price of the bond. This is written as:

where

and

Then,

and

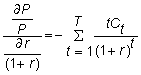
Formally, the lefthand side is the elasticity of the bond price with respect to (1 + r). It measures the percentage change in the bond price due to a percentage change in

(1 + r). It also has another interpretation. Note that

is the present value of the cash flow in period t. Because

we get

so that

is the share of the price contributed by the cash flow at time t. Then, we can write

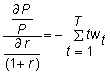
and since

this elasticity equals the weighted average time to maturity, where the weights are the w. Macaulay's duration is defined by

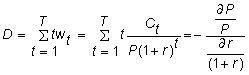
Note that the duration of a zero-coupon bond equals the maturity of the bond, while the duration of a coupon bond is less than the maturity.

The bond immunization theorem (first derived by Samuelson) states that interest rate risk can be hedged by matching the duration of a bond with the desired holding period. The proof of this theorem exploits the fact that bond prices move inversely with interest rate risk, and that bonds of different maturities react differently to interest rate changes. As a result, if rates increase, reinvestment of a coupon can be made at higher rates, but the market value of the bond decreases; the reverse is true for a rate decrease.

We illustrate the argument using the case of a single liability, C payable at time t. Let r denote the (constant) yield to maturity. Then, the present value of the liability is

and it has duration equal to t. We will call this the first bond.

We will call the portfolio of these zero-coupon bonds the second bond. Assume that

Consider the present value of the bond as a function of the interest rate of two different cash flows:

At the end of ten years, the cash flow is $109. There is no other cash flow.

There is a cash flow of $22 at the end of Year 2 and a cash flow of $135 at the end of Year 18. There are no other cash flows.

Alternative A has a duration of 10. If the interest rate is 12%, then Alternative B also has a duration of 10. Note that even though we know the duration of each component of Alternative B (2 and 18) we cannot determine the duration of the two cash flows together without reference to the interest rate. At "today’s" interest rate of 12%, both these cash flows have the same present value. The present value as a function of the interest rate is given in Table 6.1.

Note that the present values are equal at 12%, where the durations are also equal. Otherwise, at other interest rates, Alternative B is always more valuable than Alternative A.

If the yield to maturity increases, the present value of the liability falls by more than the present value of the second bond. If the yield falls, the value of the liability rises by less than the value of the second bond. Therefore, the second bond immunizes the first bond.

In Appendix 6A, the proof for the bond immunization theorem in the context of this example is formally provided.

Figure 6.4 also shows that if we measure interest rate sensitivity simply by the duration, we will generally not get an accurate measure of this sensitivity by calculating the duration. In the figure, both bonds have the same duration, but the second bond is less sensitive. This is because it is more "convex," as shown by the derivative calculation. In general, more convexity is preferred to less convexity. The convexity of a bond is the second derivative we calculated, usually normalized by either the price of the bond or twice the price of the bond.

The bond immunization theorem depends upon an unrealistic assumption about interest rate changes; that is, the change in the yield is independent of the time to maturity. For example, if yield for a one-month Treasury bill changes by 5 basis points (1/100 of 1% equals 1 basis point), then the yield for a 30-year government bond must also change by 5 basis points. This assumption is unrealistic because it permits only parallel shifts of the term structure of interest rates.

In the next topic, Application of the Bond Immunization Theorem, you will apply the theory develop to date to estimate and hedge a position that the Bond immunization theorem could develop.