6.8 Application to a Futures Example
|
I |
n this topic, we apply the theory developed in Topic 6.7 to an actual hedging example. Recall that initially, the arbitrage-free present value of the futures price is zero, but as subsequent shifts occur in interest rates, this is no longer the case. Here we consider the case of shifts in interest rates that occur subsequently to the time of settlement of the futures contract.
Example
Suppose you want to hedge the interest liability for a loan for $2 million, which is structured to pay interest every 45 days at the spot U.S. Treasury 45-day rate plus 100 basis points. Suppose that you choose to hedge this loan using standardized three-month T-bill futures contracts.
Hedging the variable interest liability on a loan is equivalent to converting a variable rate loan into a fixed rate loan if the hedge is perfect. We consider using the futures market for this conversion.
In this example, we consider the case where the critical events in the loan contract do not precisely "map" into the standardized futures contracts. As a result, the problem is to identify the extent to which the short-term standardized contract is relevant.
The standardized futures contracts, at the time of settlement, are obligations to exchange a three-month T-bill for the futures price.
Timeline of Critical Events
Day 0 is the present. Day 45 is the time, of settlement of the futures contract. At this time, the futures price is paid by the long (i.e., the side that is long futures contracts), and a 90-day T-bill is delivered by the short (the side that is short futures contracts). The value of the 90-day T-bill is determined from the spot 90-day rate from Day 46 to Day 135.
On Day 45, the first interest payment is made on the loan. The interest is determined from the 45-day spot rate for the period from Day 46 to Day 90.
Define Period 1 as the time from day 1 to Day 45, Period 2 as the time from Day 46 to Day 90, and Period 3 as the time from Day 91 to Day 135.
Assume that the realized spot rate of interest for Period 1 is 3.75% and that the day count for computations is 360.
At the time of settlement, the value of the underlying security for the futures contract is determined from the realized spot 90-day T-bill rate. It is this rate that is used to hedge the realized spot 45-day rate plus 100 basis points. As a result, the example applies to the case where the timing of the cash flows cannot be exactly matched.
Table 6.2 shows the projected population of Treasury 45-day yield realizations for Period 2. The market’s expected forward Treasury rate for Period 3 is 0.0375. Further, according to the unbiased expectations theory of the term structure, let us assume that forward rates equal expected future spot rates
Table 6.2
Projected Treasury Rates: Period 2
|
Projected Treasury Rates for Period 2 |
|
0.0200 |
|
0.0300 |
|
0.0375 |
|
0.0450 |
|
0.0550 |
Given this assumption the forward rate used by the market for Period 3 is 0.0375 and the expected spot rate for Period 2, from Table 6.2, is also 0.0375. These rates are used to construct the arbitrage-free value of the 90-day futures contracts at the beginning of Period 1.
That is, the present value of the futures contract, F, at the beginning of Period 1, using these rates, is zero.
For these rates, we can construct a simple schedule of possible realized values for the interest expense and the security that is accepted for settlement of the future’s contract.
Let the possible set of realized Treasury rates plus 100 basis points for the 45-day Period-2 rate at the time of the first interest payment be as in Table 6.3. That is, the first column equals Table 6.2 plus 100 basis points (i.e., 0.01).
Table 6.3
Treasury Rates: Period 2
|
Treasury + 100bps |
Realized Interest Expense |
Future’s Settlement Value |
Future's Price (f) Given Expected Rates |
|
0.0300 |
$7,500 |
$992.8522 |
$990.6905 |
|
0.0400 |
$10,000 |
$991.6158 |
$990.6905 |
|
0.0475 |
$11,875 |
$990.6905 |
$990.6905 |
|
0.0550 |
$13,750 |
$989.7669 |
$990.6905 |
|
0.0650 |
$16,250 |
$988.5382 |
$990.6905 |
In Table 6.3, the realized interest expense equals the realized interest on the $2-million dollar loan. For example, the $10,000 in row 2 is computed as follows:
![]()
which you can verify equals $10,000. The remaining realized expense entries can be verified from the same type of methodology.
Next, you can verify the future's settlement value equals the value of the 90-day T-bill at this time. For example, the value of the T-bill, if the expected spot rates under the unbiased expectations theory of the term structure equal 0.0375 for Periods 2 and 3, is:
![]()
Similarly, for the case where the realized 45-day rate equals 0.03 and the 45-day forward rate (by assumption) equals 0.0375, the future’s price is:
![]()
In this example, the arbitrage-free futures price, f, is such that the net present value, under the unbiased expectations theory, equals zero. Therefore, the futures price equals $990.69.
Table 6.4
Future’s Price Sensitivity to Different Period-2 Rates
|
Period-2 Rates |
Future’s Settlement Value |
Future's Price Change from Current Price ( Df) |
PV of Future’s Price Change from Current Price ( DF) |
|
0.0200 |
$992.8522 |
$2.1617 |
$2.1516 |
|
0.0300 |
$991.6158 |
$0.9253 |
$0.9210 |
|
0.0375 |
$990.6905 |
$0.0 |
$0.0 |
|
0.0450 |
$989.7669 |
-$0.9236 |
-$0.9184 |
|
0.0550 |
$988.5382 |
-$2.1523 |
-$2.1422 |
The present value is computed using the Period-1 spot rate of interest (1+0.0375/8).
Construction of the Hedged Position
The hedged position using futures can be expressed as:
![]()
where V is the value of the hedge, S is the underlying position’s spot value, F is the present value of the futures contract, and n
f is the hedge ratio. In the example, the underlying spot rate is the interest expense paid at the end of Period 1.Calculate the first-order differences from the difference between the future’s settlement price as the interest rates change from 0.03 to 0.04, etc., in Table 6.3. The present value of these differences can be calculated as, in Table 6.4.
Table 6.5
Changes in f and F
|
Sensitivity Analysis: Treasury Rates Period 2 |
Change in Futures Price Given Change in Period 2 Rate |
Change in P.V. of futures Price |
|
0.02-0.03 |
1.2364 |
1.2306 |
|
0.03-0.0375 |
0.9253 |
0.9210 |
|
no change |
0.00 |
0.00 |
|
0.0375-0.045 |
-0.9236 |
-0.9193 |
|
0.045-0.055 |
-1.2287 |
-1.2229 |
The values in Table 6.5 are computed from the row differences in Table 6.4.
The ratio of these changes (change in F for a change in f) is approximately 1 as required by the assumption of compounding in continuous time in Topic 6.7.
Now assume the discrete form of the hedge ratio derived in Topic 6.7, which is:
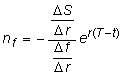
Table 6.6
Changes in f and F
|
Sensitivity Analysis: Treasury Rates in Period 2 |
Change in Future’s Price Given Change in Period-2 Rate |
D f/Dr |
Change in Spot Price |
D F/Dr |
|
0.02-0.03 |
1.2364 |
123.64 |
1.2306 |
$123.06 |
|
0.03-0.0375 |
0.9253 |
123.3733 |
0.9210 |
$122.80 |
|
no change |
0.00 |
0.00 |
||
|
0.0375-0.045 |
-0.9236 |
123.1467 |
-0.9193 |
-$122.57 |
|
0.045-0.055 |
-1.2287 |
-122.87 |
-1.2229 |
-$122.30 |
The change in the spot value in Table 6.7 is computed from the change in the present value of the settlement price for the underlying spot rate.
Table 6.7
Changes in the Underlying Spot Rate
|
PV Settlement Value |
Settlement Value |
|
$988.22 |
$992.8522 |
|
$986.99 |
$991.6158 |
|
$986.07 |
$990.6905 |
|
$985.15 |
$989.7669 |
|
$983.93 |
$988.5382 |
That is, in this example, the number of futures contracts is calculated from:
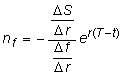
By averaging over the ratios in Table 6.6 and multiplying by the future value weight, the number of futures contracts is -1. That is, to hedge the original loan of $2,000,000 with futures on bonds with a face value equal to $1000 is 2,000 futures contracts.
To complete this example, in Table 6.8 we compare the interest expense at the end of 45 days for both the hedged (shorting 2,000 futures) and the unhedged positions.
Table 6.8 Expense Comparisons
|
Treasury + 100 bp |
Realized Interest Expense (Unhedged) |
Future’s Settlement Value |
Deviation from Future’s Price |
Total Interest Expense Less 2,000 Futures Settlement |
|
0.0300 |
$7500 |
$992.85 |
$2.1617 |
$11,823 |
|
0.0400 |
$10000 |
$991.62 |
$0.9253 |
$11,851 |
|
0.0475 |
$11875 |
$990.69 |
$0.0 |
$11,875 |
|
0.0550 |
$13750 |
$989.77 |
-$0.9236 |
$11,903 |
|
0.0650 |
$16250 |
$988.54 |
-$2.1523 |
$11,945 |
Hedging using the partial derivative hedge ratio results in an almost fixed-rate interest loan for around 4.75% annualized. The total interest expense in Table 6.8 is computed from the total variable interest (column 2) less the net cash transfer to the short at the time of settlement.
In the above example, we constructed an approximately fixed-rate loan from a variable-rate loan. By applying the reverse type of hedge, you can see that a variable-rate loan also can be constructed from a fixed-rate loan. These types of exercises provide an important way of hedging interest rate risk in a swap book. A "vanilla" interest rate swap is a contract that has two counter-parties, A and B, who agree to swap fixed and variable interest payments over time relative to some stated notional principal (i.e., face value). For example, Counter-party A buys variable and sells fixed and Counter-party B does the reverse. Intermediaries that make market swaps make profits from their quoted spreads. Generally, they cannot line up both sides at the same point in time. As a result, one risk they face is that if interest rates move 4 basis points, for example, this can eliminate their profit margin, which also can be measured in basis points. As a result, hedging variable interest rate exposures (generally at a macro aggregate book level) in the futures market is one way of managing this source of risk.
In the next topic, Minimum-Variance Hedge Ratios, we will continue this example and contrast the partial-derivative approach with the minimum-variance approach.
 office (412)
9679367
office (412)
9679367