6.9 Minimum-Variance Hedge Ratios
|
T |
he minimum-variance hedge ratio method takes either a purely statistical approach to the problem of constructing the hedge ratio or an analytical approach if important inputs can be estimated by analytical means. It works if there is a reasonably stable linear relationship between the change in the value of the position and the change in the value of some hedging instrument.
Recall that the hedging instrument is the security or portfolio used to alter the exposure of the underlying position to interest rate risk. The minimum-variance method assumes that the hedging instrument has been selected and is applied empirically, by using historical returns to construct the minimum-variance hedge ratio, or analytically, by using the valuation model to estimate the population values for the variance and covariance of returns. The assumption of a linear relationship implies that a constant hedge ratio can be estimated and applied independently of the magnitude of the position’s value.
If stable linear relationships fail to hold, this technique may not provide very reliable numerical estimates for the hedge ratio.
Notation
Let V
t be the value of the hedged position, St be the value of the underlying position, and HI be the value of the hedging instrument, at time t. Let the hedge ratio that applies to the hedging instrument be nhi.At any given time, the value of the hedged portfolio, V
t, is defined as:![]()
and the change in these portfolio values from time t to time t + 1 is:
![]()
The objective of this approach is to choose n
HI to minimize the variance of the change in the hedged portfolio’s value.The variance of the change in the hedged portfolio’s value as a function of n
HI is defined as:![]()
The unconstrained optimization problem is formally stated as:
![]()
The first-order condition with respect to the decision variable, n
HI, is: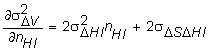
The second-order condition is strictly positive:
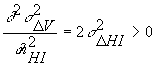
Setting the first-order condition to zero and solving for n
HI yields the minimum-variance hedge ratio: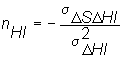
Example: Minimum-Variance Hedging of a Variable-Rate Loan
Hedging interest rate risk can be thought of as converting some type of variable- rate loan into a fixed-rate loan. Very often the timing of the cash flows in the underlying position do not match well the timing of cash flows associated with standardized securities, such as futures.
As a result, even though theoretical hedge ratios may be estimated, risk arises from a nonalignment of the timing of cash flows for both the underlying position and the hedging instrument.
Consider hedging the interest liability for a loan, for $2 million, which is structured to pay interest every 45 days at the spot U.S. Treasury rate plus 100 basis points. Suppose you choose to hedge this loan using standardized three-month T-bill futures contracts.
The standardized futures contracts, at the time of settlement, are obligations to exchange a 3-month T-bill for the futures price.
The critical events are as follows:
Day 0 is the present. Day 45 is the time of settlement of the futures contract. At this time, the futures price is paid by the long, and a 90-day T-bill is delivered by the short. The value of the 90-day T-bill is determined from the spot 90-day rate from Day 46 to Day 135.
On Day 45, the first interest payment is made on the loan. The interest is determined from the 45-day spot rate for the period from Day 46 to Day 90.
Define Period 1 as the time from Day 1 to Day 45, Period 2 as the time from Day 46 to Day 90, and Period 3 as the time from Day 91 to Day 135.
Assume that the realized spot rate of interest for Period 1 is 5% and that the day count for computations is 360.
Suppose that the goal is to minimize the variability of the interest expense.
The population of Treasury yield realizations for the first 45-day period is as projected in Table 6.9.
Table 6.9 Treasury Rate Projections
|
Projected Treasury Rates for Period 1 |
|
0.0200 |
|
0.0300 |
|
0.0375 |
|
0.0450 |
|
0.0550 |
Assume also that the market’s expected forward Treasury rate for Period 2 is 0.0375. Suppose the market uses this forward rate to value the 90-day futures contracts.
For these rates, we can construct a simple schedule of possible realized values for the interest expense and the security that is accepted for settlement of the futures contract.
Let the possible set of realized Treasury plus 100 basis points, for the 45-day rate at the time of the first interest payment, be as in Table 6.10.
Table 6.10 Possible Realizations at time of 1st Interest Payment
|
Treasury + 100bps |
Realized Interest Expense |
Future’s Settlement Value |
|
0.0300 |
$7,500 |
$992.85 |
|
0.0400 |
$10,000 |
$991.62 |
|
0.0475 |
$11,875 |
$990.69 |
|
0.0550 |
$13,750 |
$989.77 |
|
0.0650 |
$16.250 |
$988.54 |
The first-order differences in Table 6.11 are calculated in Table 6.12.
Table 6.11 First-Order Differences
|
Change in Treasury + 100 bp |
Change in Interest Expense |
Change in Forward Settlement |
|
0.04 - 0.03 |
$2,500 |
$-1.236 |
|
0.0475 - 0.04 |
$1,875 |
$-0.925 |
|
0.055 - 0.0475 |
$1,875 |
$-0.923 |
|
0.065 - 0.055 |
$2500 |
$-1.229 |
If each rate is assumed equally likely, the variance of the change in the interest expense is 97,656.25; the variance of the change in the future’s settlement value is 0.0238; and the covariance between these two first-difference variables is -48.2301.
Recall that the minimum-variance hedge ratio is:
![]()
By substitution, the estimated hedge ratio is:
![]()
To convert this variable-rate loan to an approximate fixed-interest loan requires that you short 2025.37 futures contracts.
To complete this example, in Table 6.12 we compare the interest expense at the end of 45 days for both the hedged (shorting 2025.37 futures) and the unhedged positions.
Table 6.12 Expense Comparisons
|
Treasury + 100 bp |
Realized Interest Expense (unhedged) |
Future’s Settlement Value |
Deviation from Future’s Price |
Total Interest Expense Less 2025.37 Future’s Settlement |
|
0.0300 |
$7500 |
$992.85 |
$2.16 |
$11,875 |
|
0.0400 |
$10000 |
$991.62 |
$0.93 |
$11,884 |
|
0.0475 |
$11875 |
$990.69 |
$0.00 |
$11,875 |
|
0.0550 |
$13750 |
$989.77 |
($0.92) |
$11,887 |
|
0.0650 |
$16250 |
$988.54 |
($2.15) |
$11,895 |
Hedging using the minimum-variance hedge ratio results in an almost fixed-rate interest loan for around 4.75% annualized. The total interest expense in Table 6.12 is computed from the total variable interest (column 2) less the net cash transfer to the short at the time of settlement.
An alternative is to enter into a variable-for-fixed plain vanilla swap. You should be able to see that the ability to hedge in the very liquid futures markets places a bound on the pricing of an equivalent vanilla swap. That is, there should be no difference in hedging the variable interest rate risk using vanilla swaps or futures contracts.
It is interesting to contrast the results from the partial-derivative approach with that of the minimum-variance approach. For this example, the minimum-variance approach worked slightly better than the partial-derivative approach.
Other Risk/Return Possibilities
Most investment firms do not choose to minimize their variance. In general, institutions that want to hedge interest rate risk tend to prefer some other possibility between no-hedging and the minimum-variance hedge. Different strategies can be valued in a straightforward manner by observing the interest rate risk/return opportunities as the number of futures contracts is varied from 0 to 2025.37. Once you select more than 2025.37, you have chosen a portfolio that is dominated by some other portfolio.
 office (412)
9679367
office (412)
9679367